причем для каждого из слагаемых обратное z-преобразование

Таким образом, если

f(Z):

Я(2)

N (г)

причем R(z) и N(z) -полиномы относительно г, а степень полинома числителя не превышает степени полинома знаменателя и, кроме того, полином N(z)=0 не имеет нулевых и кратных корней, то искомое решение

Здесь zv - корни полинома N(z)=0, а dN(z)

Часто правая часть уравнений 21-73 и 21-73а представляет собой единичную решетчатую функцию 1[я7 п], для которой z-преобразование

Z{\\r£Tn\}=-.

z - 1

Тогда F(z) имеет следующий вид: M(z) z

F (z) =

N(z) z - \

В этом случае решение находится по формуле, вполне аналогичной второй формуле Хевисайда для обычного преобразования Лапласа (см. т. 1, стр. 542). Если для М(г) справедливы сформулированные выше условия, то

М (0)

/V(0)

M(zv)

(l-zv)/V(zv)

где zv - по-прежнему корни уравнения . N(z)=0.

Таким образом, нахождение решения разностных уравнений благодаря z-преоб-разованию сводится к сравнительно простым алгебраическим операциям, наиболее трудная из которых - отыскание корней полинома N(z)=0.

21-9. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ИМПУЛЬСНЫХ СИСТЕМ

Импульсная передаточная функция

Рассмотрим цепь, состоящую из 6-клю-ча (Ь-Кл) и фильтра с передаточной функ-

цией W(p) (рис. 21-77, а). К такой цепи, как было показано ранее, можно свё*сти системы с практически любым импульсным элементом. После 8-Кл входной сигнал f(t) преобразуется в сигнал f*(t), представляющий собой последовательность модулированных по площади 6-функций (см. стр. 86):

f*(t) = f(t)8T(t) =

= Е f\kTn\b(t-kTa).

Найдем модифицированное z-преобразование выходного сигнала y(t), т. е.

. Рнс. 21-77. Импульсная передаточная функция

а - получение функций со звездочкой на входе и выходе: б - представление звена импульсной передаточной функцией W(z) = Y(z)/F(z).

Пусть g(t) обозначает импульсную переходную функцию фильтра W(p), т. е. является реакцией этого фильтра на б-функцию. Связь между g(t) и W(p) определяется преобразованием Лапласа (см. стр. 17):

W(p)=J g (0 e~pt dt = L{g (/)} о

g(t) = L-*{W(p)}.

Выходная величина y(t) в любой момент времени t может быть найдена в соответствии с принципом наложения по формуле

y(t)= £ g(t-kTn)f[kTn]. (21-74)

Значение выходной величины в дискретные равноотстоящие промежутки времени г=и7 п+е7 д, где 0 <е<1:

у1пТп + еТп] = у[п, е] =

= Е f[nTn]glnTn + eTn.-kTn] =

= 2 f[nTn]g[(n-k)Tn+eTn].

Применим к последнему равенству модифицированное 2-преобразование. Тогда, учитывая формулу свертки (21-70), получаем:

Y(z, е) = W(z, e)F(z), (21-75)

Y(z, e) = Ze [у[пТа + еТп]}

- z-преобразование выхода фильтра;

F(z) - Z{f[nr ]}

- z-преобразование решетчатой функции /[nTVJ, а

W(z, e) = Z{gr[(n + e)rn]} =

= 2 g[(n + e)Ta]z-n

- модифицированное z-преобразование от решетчатой функции, полученной из импульсной переходной характеристики. В частности, при s=0

Y(z) = W(z)F(z) (21-76)

W (г)= Z [g [пТп]} = Е д [пТв] z~n.

Функция W(z, е) или W(z) называется импульсной передаточной функцией или z-передаточной функцией фильтра W(p).

Импульсная передаточная функция представляет собой отношение модифицированного z-преобразования выходной величины У(г, е) к z-преобразованию входной величины F(z).

Чтобы вычислить импульсную передаточную функцию фильтра, необходимо:

определить импульсную характеристику фильтра g(t) (как обратное преобразование Лапласа от передаточной функции

записать решетчатую функцию g[nTu] или е?[(л+в)Гп], т. е. вместо t подставить дискретные величины t=nTrl или t- = (ft-f-e)7 ;

найти z-преобразование от g[nTu] или модифицированное z-преобразование от g[(n+e)Tu],T. е.

W(z) = Е g[nTn]z-n

W(z, е)= Е g[(n + e)Tn\z-n-

Из последних соотношений видно, что W(z, е) определяется только свойствами самой цепи (характером функции g(t)) и не зависит от вида входного сигнала.

Если известна импульсная передаточная функция W(z, е) и z-преобразование F(z) входного сигнала, то, пользуясь формулой (21-75), легко найти z-преобразование У(г, е) выходной величины, а затем,

перейдя к оригиналам, можно вычислить значения выходной величины для дискретных равноотстоящих моментов времени г= =пТи+бТп (е зафиксировано). Для того чтобы определить значения выходной величины в любой фиксированный момент периода, необходимо найти ее значение для всех е. Часто достаточно знать выходную величину для е=0, т. е. решетчатую функцию у[пТп]. За счет потери информации в интервалах между импульсами достигается значительное упрощение вычислений выходной величины, поскольку практически использование аппарата z-преобразований намного проще непосредственных вычислений по формуле (21-74).

Заметим, что иногда в литературе встречается запись

W(z) = Z{W(p)},

которая отображает тот факт, что W(z) является z-преобразованием от функции g[nTn], полученной в результате обратного преобразования Лапласа от W(p). Эта запись является чисто условной. Она указывает на то, что z-преобразование производится над импульсной (весовой) решетчатой функцией g[nTu] звена, имеющего передаточную функцию W(p) (так как g(t) есть реакция звена с передаточной функцией №(р) на б-функцию). Конечно,

W(z) Ф W(p),

т. е. W(z) нельзя получить заменой в W(p) параметра р на 2. Это разные функции.

Выше было показано, что z-преобразо-вапне для функции г/[пГд] является обычным преобразованием Лапласа функции

y*(t) при замене р = -1пг:

L{y*(t))=Y(z)\ .

г=ср п

Это и дает возможность изображать на входе звена W(p) функцию f*(t), образованную преобразованием функции fit) б-ключом.

С другой стороны, из рис. 21-77, а следует, что

У(Р) = W(p)F*(p),

где.

F*(p) = L{f*(t)}.

Формально обе части этого равенства можно подвергнуть z-преобразованию, т. е. записать:

Z{Y(p)} = Z{W(p)F*(p)}. (21-77)

Левая часть равенства здесь обозначает 2-преобразование от сигнала у[пТв\, образованного из функции 1/(0 > изображение Лапласа которой равно Y(p)=L{y(t)}, т. е. Y(z).

Сопоставляя (21-77) и (21-76), получаем:

Z{W(p)F*(p)} = W(z)F(z).

Или, учитывая что F* (р)\ у = F (г), р= =- 1пг

(21 -77а,

Последняя формула показывает, что z-npe-образоваяие произведения двух преобразований Лапласа, из которых одно - переда-

S-Кл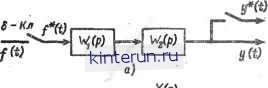

F(z) г--1 rw

w > W(z) г- *-

Рис. 21-78. Импульсная передаточная функция соединения двух звеньев.

о-- исходная схема; б - представление звена импульсной передаточной функцией.

W,(z) = Z{W1(p)}; W2(z) = Z{W2(p)}.

Таким образом, импульсная передаточная функция произведения звеньев не равна произведению импульсных передаточных функций отдельных звеньев.

Иногда приходится рассматривать систему, в которой имеется запаздывающее звено с передаточной функцией №з(р)=е~рха где т3-время запаздывания (рис. 21-79, а). В этом случае импульсная передаточная функция легко находится из передаточной функции W(z, е), т. е. по модифицированному z-преобразо-ванию:

Ze {Г(Р)}=Г(2,8).

Если запаздывание т3<7п, то передаточная функция системы с запаздыванием

-(z, l+s-y),

Wx (г, е) =

точная функция W(p), а другое - преобразование Лапласа функции со звездочкой , находится как произведение последней (при

замене р на In z) на импульсную пере-

даточиую функцию.

Рассмотрим далее схему на рис. 21-78, состоящую из двух звеньев: W\(jt) и W2(р) и Ь-Кл. Найдем z-преобразование выходной величины, т. е.

Y(z) =Z{y[nTn\} = L{y*(t)}.

Из рис. 21-78, а следует, что

У(р) = B7i(p)W2(p)F*(p).

Подвергая это уравнение Z-преобразо-ванию в соответствии со сформулированным правилом, запишем:

Y(z) = Z{W1(p)W2(p)} f*(p)\ i =

Р- у, II1Z

если 0 8 < у; W(z,e-y); если у 8 < 1,

где у=Хз/Т11 - относительное время запаздывания.

8-Кл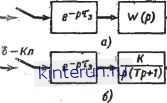

Здесь

Z{W1(p)W2(p)}f(z).

ZlWiWzip)} = W{z).

- импульсная передаточная функция звена W(p) = Wi(p)W2(p), которая может быть найдена в соответствии с правилом, сформулированным на стр. 99. Соответственно модифицированное z-преобразова-нйе:

у (г, в) = 2Е {W1 (р) W& (р)} f (z),

где 2g - обозначение модифицированного 8-преобразования от передаточной функции W(p) = Wi(p)W2(p).

Необходимо отметить, что

Z{H7,(p)W2(p)} = W(z) Ф Ф Wi(z)U72(2),

Рис. 21-79. Структурная схема системы с запаздыванием.

- общая схема; б - схема для расчетного примера.

Если требуется найти импульсную передаточную функцию с запаздыванием при 8=0, то последнее выражение упрощается и

Wx(z) = z-lW&,\-y).

Таким образом, импульсная передаточная функция системы с запаздыванием находится путем подстановки в модифицированную импульсную передаточную функцию вместо 8 значения 1-у и умножения результата на zrl.

Пример 1. Записать импульсную передаточную функцию инерционного звена (рис. 21-20)

W(p)-

Тр + 1 р + а

] Т