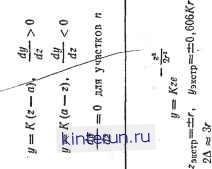
oj о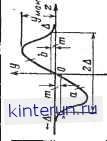

1 °-

2 f-

га o.

аз к x

g ra t-У я и

весия х0, уо называется устойчивым, если для любой области е, окружающей эту точку Хо, Уо, существует такая область начальных отклонений 6(б), что возмущенное движение, начавшееся в области 6, не достигнет границ области б. Если такую область б указать нельзя, т. е. если любое возмущенное движение достигает границ области е то состояние равновесия будет неустойчи-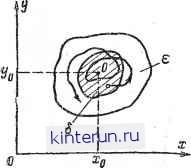

Рис. 21-94. Диаграмма, иллюстрирующая понятие устойчивости по Ляпунову.

о - равновесное состояние; показана траектория изображающей точки е и области б.

вым. Условия устойчивости, требуют, чтобы движение, начавшееся внутри б, не достигало границ области б; однако совершенно не обязательно, чтобы возмущенное движение стремилось к состоянию равновесия О (если это происходит, система является асимптотически устойчивой). В принципе возможны случаи, когда возмущенное движение около устойчивого состояния равновесия не затухает , а продолжается сколь угодно долго, причем амплитуда возмущенного движения будет тем меньше, чем меньше величина начального откло-юния

Понятие устойчивости, введенное Ляпуновым, является весьма плодотворным, поскольку оно позволяет сравнительно прости определять устойчивость состояний равновесия широкого класса нелинейных систем. Более того, понятие устойчивости по Ляпунову применимо и к периодическим движениям, которые также могут быть устойчивыми (автоколебания) или неустойчивыми.

Для того чтобы установить, является ли состояние равновесия нелинейной системы устойчивым согласно одному из методов Ляпунова:

а) находятся уравнения первого приближения, которые получаются путем линеаризации характеристики F(z) нелинейного элемента вблизи состояния равновесия 20. Процедура такой линеаризации очень проста и состоит в разложении функций в ряд Тейлора у точки z=z0, в котором удерживаются только два члена:

F (z) = F(z0)

т. е. фактически сводится к нахождению производной от F в точке го. Это соответствует замене нелинейной характеристики касательной в точке равновесия (см. рис. 21-12). Для полученной в результате линейной системы составляется передаточная функция (что эквивалентно составлению уравнений первого приближения);

б) определяется (с помощью любого из известных критериев), будет ли полученная линейная система устойчива. В том случае, если линейная система устойчива (это соответствует отрицательным вещественным частям характеристического уравнения), состояние равновесия исходной нелинейной системы будет асимптотически устойчивым. Если линейная система неустойчива (это соответствует наличию хотя бы одного корня характеристического уравнения с положительной вещественной частью), то состояние равновесия исходной нелинейной системы неустойчиво. И только в том случае, когда линейная система находится на границе устойчивости (все корни - мнимые), рассматриваемый метод Ляпунова не дает ответа на вопрос об устойчивости состояний равновесия исходной нелинейной системы и требуется дополнительно исследование.

Метод Ляпунова нельзя применять для нелинейностей, у которых в состоянии равновесия ие существует производных (например, для релейных нелинейностей).

w(s)

S(T,])+l)(II+l)

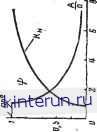
Рис. 21-95- Определение состояний равновесия нелинейной системы.

а - исходная структурная схема; б - характеристика нелинейного элемента ИЭ =cos zc.

Пример. Рассмотрим систему, структурная схема которой представлена на рис. 21-95,а, причем нелинейный элемент описывается косииусоидальной зависимостью u=cosz (рис. 21-95,6). К такой схеме сводится система фазовой подстройки частоты (см. стр. 169).

Пусть сигнал на входе изменяется с по: стоянной скоростью ve, т е. x=v0t. В системе возможны состояния равновесия при постоянном значении z=z0. Это будет в том случае, когда выходной сигнал у изменяется также со скоростью vo и на входе НЭ соответственно будет постоянный сигнал и=и0, изменяющий величину у со скоростью v0, т. е. (dy/dt)yc? = vD и vD= =KvUo- Таким образом, в системе имеется бесчисленное множество состояний равновесия, определяемых равенством:

о = cos z0 или

z0 = arccosuo = +Zp±2ferc (21-139)

и соответствующих точкам У и Я пересечения прямой и=щ с косинусоидой u=cosz. Здесь zp=arccosu0 - главное значение обратной тригонометрической функции. Каждое из состояний У к Н повторяется с периодом 2я.

В соответствии с рассмотренной процедурой линеаризуем систему у состояний равновесия У и Н, разлагая функцию u=cosz у состояний, определяемых выражением (21-139). Тогда

u = u0 +

\ dz Jz

Следовательно, нелинейный элемент у состояний равновесия заменяется пропорциональным звеном с коэффициентами передачи:

для состояний У

Г7~) = - sinz0 = - sin(-zp) = KP; \ dz lze

для состояний Н: (du\

- I =--sinz0 = - sinzp = -- /Ср. \ dz Jzn

Тогда структурная схема системы, справедливая для небольших отклонений от состояний равновесия, будет отличаться от исходной тем, что нелинейный элемент заменяется линейным с коэффициентом передачи /Ср для состояний У И -/Ср для состояний Н. Ясно, что состояния Н будут неустойчивыми для любых значений параметров линейной части W{D), так как эти состояния соответствуют отрицательным значениям коэффициента передачи Kv= =-ККр- Чтобы найти условия, при которых состояния У будут устойчивыми, достаточно записать характеристическое уравнение замкнутой системы (см. пример на стр. 51): T,X3+(T,-f T2)№+X+Kv=0 и воспользоваться, алгебраическим критерием. Тогда найдем Kv<l/Ti + l/T2-KKp- Следовательно, при Кг><ККр исходная нелинейная система устойчива, при Къ>Ккр - неустойчива. Только при /Сг? - Ккр никаких суждений об устойчивости состояний равновесия у исходной нелинейной системы сделать нельзя. Очевидно, не представляет

труда определить условия устойчивости при любой передаточной функции W(D).

Метод фазового пространства

Для исследования свойств нелинейных систем часто используется метод фазового пространства, с помощью которого можно получить наглядное представление о процессах для различных исходных состояний системы. Этот1 метод развит, главным образом, трудами советской школы физиков. Последовательное применение метода фазового пространства для решения многих важных задач теории колебаний дано в фундаментальной монографии А. А. Андронова, А. А. Витта и С. Э. Хай-кина [Л. 21].

Метод фазового пространства применим к автономным систем.ам, т. е. таким, для которых правые части уравнений, описывающих эти системы, не зависят явно от времени.

У к Фь(*1, *2, Хп),

k - 1, 2, .... п (21-140)

Требование автономности является существенным и физически означает, что все внешние воздействия на систему полагаются постоянными, а движения в системе обусловлены только внутренними силами.

Наиболее наглядные результаты этот метод дает в случае исследования систем, описываемых уравнениям первого н второго порядка. В последнем случае состояния системы можно описать двумя параметрами, а полную картину процессов в системе отобразить на плоскости. Отсюда происходит другое, распространенное название: метод фазовой плоскости. Для систем более высокого порядка метод теряет свою наглядность, хотя в принципе его можно использовать и в этом случае.

Движение системы в фазовом пространстве отображается перемещением точки, характеризующей состояние системы, по некоторым так называемым фазовым траекториям. Совокупность фазовых траекторий, описывающих все характерные (или возможные) движения системы, называют фазовым портретом системы.

В некоторых случаях практики интересуются лишь характером движений системы (качественный анализ); в этих случаях метод фазовой плоскости является очень эффективным.

Поясним существо метода фазового пространства на примерах нелинейных систем 1-го и 2-го порядка.

Системы первого порядка. Примем, что система автономна и ее поведение описывается нелинейным дифференциальным уравнением первого порядка

(21-141)

щая внешнее воздействие на систему. Состояние системы в каждый данный момент определяется величиной самой координаты х dx

и скорости у= -- =х. Переменные в урав-dt

нении (21-141) разделяются, и общее решение имеет вид:

С dx J Ф (х, а)

+ С.

(21-142)

Здесь С - постоянная интегрирования, соответствующая заданным начальным условиям (г=0, х=хо).

Во многих случаях, однако, удобнее не вычислять интеграл (21-142), а* рассмотреть свойства системы на фазовой плоскости х, у=х=*ф(х, а).

Уравнение (21-141) определяет (для каждого заданного значения а) линию на плоскости х, у (рис. 21-96, а), которая и яв-

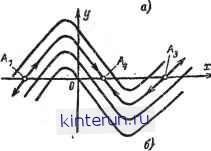Здесь ф - нелинейная функция величины х, а а - постоянная величина, характеризую-

Рис. 21-96. Фазовый портрет системы первого порядка.

а - фазовый портрет системы, в которой возможны периодические движения; б - семейство фазовых траекторий, соответствующих различным постоянным управляющим воздействиям (здесь периодические движения невозможны). Состояния А\, А2, Аз -г неустойчивы. А, - устойчиво.

ляется фазовой траекторией системы. Действительно, для любой точки А этой линии уравнение (21-141) удовлетворяется, с другой стороны, любая другая точка плоскости (например, В) не удовлетворяет данному уравнению. Таким образом, рабочая точка, отвечающая решению уравнения, двигается только по кривой тт. Последняя отображает все возможные движения в системе,