Сравнивая это выражение с ошибкой для некомплексной системы (которая получается, если в (22-60) положить Я=0)

0вос = тт- хр - Т; , (22-61)

1 + W

легко заметить, что при одинаковой полосе системы динамическая ошибка в некомплексной системе будет больше, чем в комплексной. Эта разница тем значительнее, чем быстрее изменяется составляющая ха по сравнению с хи. (Например, различие будет велико при определении координат малоподвижного корабля с быстр од вижущегося самолета.)

Выражения для ошибок, обусловленных действием помехи Яр радиотехнической системы, в обеих системах одинаковы. Правда, в комплексной системе присутствует дополнительная ошибка, обусловленная погрешностью Яа измерителя собственного движения. Необходимо поэтому оценить величину этой ошибки и степень ухудшения общей точности, обусловленной указанной погрешностью.

Для выяснения этого сначала необходимо решить задачу о возможности получения выигрыша в точности при измерении с помощью двух измерителей одной и той же величины. В нашем случае такой величиной является координата ха. Поэтому, положив в (22-60) хц=0, получим выражение для ошибки измерения величины ха двумя системами, обладающими первичными ошибками Яр и Яа:

®вое.к =-~- Г~ЯП- . .--Я =

1 +

1 + W

= -[ФЯр + (1-Ф)Яа].

Такой же результат для погрешности получается в схемах фильтрации и компенсации обработки измерений двух измерителей (рис. 22-117).

хвых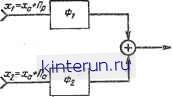

jCz=xa+f!B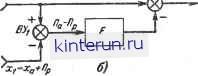

Рис. 22-117. Схема объединения двух и мерителей одной величины.

о - схема фильтрации; б - схема компенсации.

В схеме фильтрации (рис. 22-117, а) имеются два фильтра Фг и Фг, через которые пропускаются сигналы X\ = xa + nv и Х2=ха+Па. Выходные сигналы суммируются так, что

Хвых = Ф\(*ь + Яр) + Ф2(*а + Яа).

Если выбрать фильтры так, чтобы Ф2= = 1-0i, и обозначить Ф4=Ф, то

Хвых = Ха + ФЯр + (1 - Ф)Яа.

Таким образом, в схеме фильтрации результирующая ошибка

= [ФЯР + (1 ф)Яа]

выражается так же, как в рассмотренной выше комплексной системе.

В схеме компенсации (рис. 22-117,6) сигналы Xi и Х2 подаются на вычитающее устройство ВУ\, где образуется разность х2-Х1=Яа-Яр, которая затем пропускается через фильтр F и вычитается из сигнала Хг (вычитающее устройство ВУг), так что

Хвых = Ха + Яа - F(IJa - Яр) = = Ха + РЯр+ (1-F)/7a.

Выбрав F=Ф, найдем, что ошибка

ха - хвых = - [ФЯр + (1 - Ф)Яа]

выражается так же, как и в рассмотренной комплексной системе.

Последняя схема позволяет дать наглядное представление о физической причине выигрыша. В результате первой операции вычитания остается только разность помех Яа-ЯР. Если эти помехи сосредоточены в различных частотных областях, например Яа - в низкочастотной, а Яр - в высокочастотной части спектра, то имеется возможность выбрать частотную характеристику фильтра F так, чтобы подавить одну из составляющих помех и пропустить другую. В нашем случае это должен быть фильтр нижних частот. Тогда пропущенная фильтром (оставшаяся) часть помехи (Яа) вычтется из сигнала ха+Па (ВУ2) и на выход пройдет сигнал ха. Степень чистоты этого сигнала определяется тем, насколько хорошо удается отфильтровать составляющую Яа от составляющей Яр и сохранить Яа после фильтра F, т. е. тем, насколько сильно разнесены спектры помех по шкале частот. Таким образом, выигрыш в точности при использовании двух измерительных уст- ройств можно получить при условии, если помехи сосредоточены в различных областях спектра.

Дисперсия ошибки воспроизведения в рассматриваемой системе

[ Sp((B)<P(/(B) *B +

+ ]4( )ii

Ф(/ш)2Ао,

где Sp(co) и Sa(a>)- спектральные плотности ошибок измерителей (радиотехнического и ИСД).

Иллюстрацию выигрыша при рассредо точении спектральных плотностей в различ-. ных частотных диапазонах дает рис. 22-118. Здесь показаны односторонние спектральные плотности входных ошибок Ga и Gp (рис. 22-118, а), квадраты частотных харак-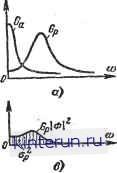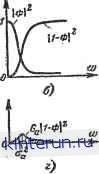

Рис. 22-118. Иллюстрация выигрыша в схемах объединения двух измерителей.

а - спектральные плотности ошибок (G

2Sp;

Ga=2Sa); б - частотные характеристики фильтров в - образование дисперсии радиотехнического из мерителя; г - образование дисперсии ИСД (дне Персии равны заштрихованным площадям).

теристик фильтров Ф2 и 1-Ф2, а также приведены результаты перемножения кривых СРФ2 и Gal-Ф2 и интегрирования полученных площадей (т. е. образование дисперсий Од и ор). В практике ошибки инерциальных и других ИСД сосредоточены обычно в узкой области частот вблизи нуля; помехи Яр широкополосны. Поэтому обычно можно выбрать частотную характеристику замкнутой следящей системы Ф(/ш) так, чтобы общая точность измерений увеличивалась по сравнению с измерением ха

только радиотехнической системой или только ИСД. (Напоминаем, что при измерении в каждой из систем нельзя выделить ха в чистом виде, а можно измерить ха лишь с динамической ошибкой.) Определение понятия выигрыш , а также некоторые количественные характеристики выигрышей и условия их получения приведены в [Л. 17].

Возвращаясь к изучению ошибок комплексных систем с учетом движения цели, сопоставим зависимость составляющих ошибок комплексной и некомплексной системы от полосы пропускания системы по формулам (22-60) и (22-61) (рис. 22-119). Из сопоставления ясно, что оптимальная полоса комплексной системы ДЕоит.к уже, а минимальная дисперсия суммарной ошибки °вос.к.мин меньше, чем в некомплексной (соответственно AFonx, свосмии). Это объясняется тем, что кривая квадратов динамической ошибки о дИИ в некомплексной системе располагается значительно выше и правее кривой Один.кв комплексной системе, поскольку считается, что спектр воздействия ха значительно шире спектра воздействия

Дополнительные ошибки са ИСД, естественно, невелики, и их спектр сосредоточен в области низких частот.

Для наглядности рассмотрим простейший пример.

Будем полагать систему астатической с передаточной функцией разомкнутой сис-

Й7(р) =

Р (Тр+1)

Положим далее спектральную плотность Sp(co) равномерной в полосе ДРЭ системы и равной плотности у нулевой частоты: (ip(co) =SP(0) =SP0), а спектральную плот-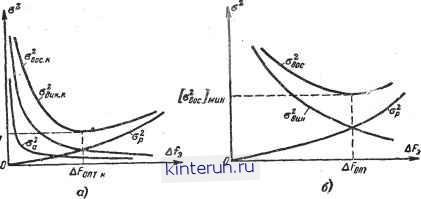

Рис. 22-119. Графики, иллюстрирующие характер изменения составляющих ошибок в зависимости от полосы Af .

с - в комплексной системе; б - в некомплексной системе.

ность ИСД, описываемой выражением (см. стр. 72),

Sa(co)

2аОо а2+ш2

причем эта спектральная плотность сосредоточена у частоты ш=0 (а мало, время корреляции велико).

Обе величины хц и ха меняются с постоянной скоростью

Хц = Vnt и Ха = Vat,

причем

Оц -С Va.

Эквивалентная полоса системы (см. стр. 75) AFB=Kv/2.

Квадраты динамической ошибки в некомплексной, и комплексной системе равны соответственно:

2 I 2

п + °а

4/ F,

ДНН.К

Дисперсия шумовой составляющей ошибки (одинакова ддр обеих систем)

°вос = Sp0 &Fa-Дисперсия ошибки ИСД

°а 2я j а

2 астп

I Гр2 + р р [Гр2+р + /С0р=/(В

dco.

Интеграл вычисляется с помощью табл. 21-7 после приведения к виду

2 сад-д (Г s2 + s) (Ts2 - s) (a+s)(a-s)(Ts2+S+K0)(n2+K0)

В результате вычислений находим: з Г(сс+ КР)+1

: aa;

сс(Гсс+1) + К0

Здесь вместо Кг> подставлено его значение /Сщ =2Д.РЭ. Общая дисперсия ошибки в комплексной системе

°вос.к = дин.к + 4 + °а-

Общая дисперсия ошибки в некомплексной системе

°вос:

Задаваясь некоторыми количественными данными (не имеющими отношения к какой-либо реальной технической задаче): оц = =0,1 ед/сек; аа=0,5 ед/сек; о = г>ц + г>а = =0,6 ед/сек; а=0,2 1/сек) of=4-10 4 ед2; Spo=2-10-5 ед2-сек, построим кривые, приведенные на рис. 22-120. Из этого примера следует, что оптимальная полоса в комплексной системе в 18/6,4 я; 3 раза, а квадрат минимальной ошибки в 5,5/2=2,25 раза меньше, чем в некомплексной системе. Результаты были бы еще более разительны, если отношение va/vn было бы большим (в приведенном примере оно составляет всего 4).

В комплексной системе оптимальная полоса может быть значительно меньше, чем в некомплексной, что ведет к снижению шумовой ошибки. При равных полосах уменьшается динамическая ошибка. Результатом этого является снижение вероятности срыва слежения при действии радиопомех высокого уровня, что, конечно, имеет большое практическое значение.

Указанное выше условие согласования ЯЙ72=1 практически можно выполнить ие всегда. Действительно, если, например, Wz(p) представляет собой инерционное звено с постоянной времени Т, то при выполнении условия согласования Я(р)=Гр+1

согласующий фильтр является идеальным форсирующим звеном, которое практически выполнить невозможно Можно использовать реальное форсирующее звено

Тр+ 1

Яр(р)=;

Учтем далее, что Kv и Т нельзя выби рать независимо, так как в противном слу- fs£j чае переходная характеристика будет не удовлетворительной. Полагая коэффициент

колебательности £ =

=0.7, на-Д,

ходим 7 Ки=1.

С учетом этого получим? a + 4AF3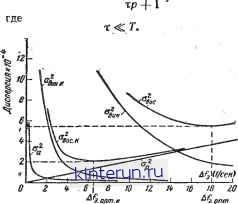

at = actf - .

o? + 2aAFa + 4AF2

Рис. 22-120. Диаграммы ошибок в комплексной и некомплектной системах (иллюстрация числового примера).