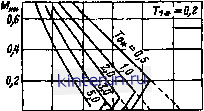Ofi 0,2

й Сг 0,4 0,В 0,8 1,0 fар*

о 0,1 0,2 0,3 0,4 0,5 fp*

0,2 0,4 0,В 0,8 1,0 f,p*

0,1 0,2

0,4 0,5 0,Bfp

0,В 0,4

0,2 0,4 0,В 0,8 1,0 fnp*

0,1 0,2 0,3 0,4 0,5 0,6fptb

Рнс. 3.48. Обобщенные двнамвческве харектервствкв вндуктвввых ШД.

последовательности. Преобразование целесо-обрааяч прн m = 4.

4. Независимо от числа фаз и характера их коммутации преобразование координат целесообразно для ШД с отдельным контуром возбуждения, так как в этом случае получаем: три уравнения, если возбунедеине осуществляется обмоткой, и два - прн постоянных магнитах иа полюсах. Размещение контура возбуждения на роторе (активные ШД) или иа статоре (индукторные ШД) ие влияет иа вид уравнений.

Определение основных характеристик ЩД - предельных нагрузочных в установившихся режимах М = if) в предельных динамических / р = Ф (Мн); /т = Ф (А*н) и /р = Ф (Afa) - выполняется по полной системе уравнений (3.20). Здесь fnps ft. fp - частоты приемистости, торможения и реверса соответственно; - момент нагрузки.

Система относительных единиц позволяет представить результаты решения системы (3.20) в виде обобщенных предельных механических фис. 3.46) и динамических (рис. 3.47 и 3.48) хактеристнк. пригодных для целого класса ШД независимо от конкретных значений параметров двигателя и нагрузки.

Система базовых значений, используемых прн описании ШД приведена в табл. 3.8, а относительных единиц - в табл. 3.9.

3 Зама 4М

Наиболее общая система уравнений для индукторного ШД с отдельной обмопюй возбуждения (общий случай записи уравнений движения) в относительных единицах, определяемых из табл. 3.8 и 3.9, и в координатах d, q, О записывается в матричнсА форме следующим образом:

н =

Характершмаш jutmmtMSM i/ponpueoda

Наоуяжеяве

Электрвчеекое сопротнвлевне Так

Пмокосцшяеаце

длектеомагввт-выЖ момерт

Врея

Электрвчесцая угловая CRO-рм*

Мехаввчееиая угловая еко-росп-

Мвщв?т

Электродввжу-

в 6

- г л

* *Ф ф

P**-oko-b.k. = bbc

.=т- *6б

Т-бб-йб. л1б

Cte А

86 И и

Гц рад/с рад/с

Модуль геометрической cyifHH одвовренвме првло-jO/fwx фазвых вапряже-вв8. приведеввцй к двум жвваалевтрыы обмоткам ареобразояаавого ЩД

Сопротивлеиве аепв фазы постояввоиу току . Ток в ццв Jiaam. включев-вой ва BewilK явса№внвгв Banpe i k , рмго базовому

Ампдитуда сосювой волны вотокйсцеш1ен9 Фазх о ковтуррм возвужденвя

Шя всех ШД. а роме чвсго реактиввш) прв уставовнв-Шцхвя токах

Амплятуда спа ческого евахроввзврующего момента

Период собственных круговых колебаний ротора ШД вместе в првсоедввеввымв маховыми массами нрнвод-вого механизма

Частота, чивлеивв Ъавнан круговой астот собствея-ных K0Jie(5 BHS ротора ШД, вэятФР0 9 .ввсгеме привода

Электрическая угловая скорость поля в ротора, численно раввав круговой частоте

Механическая угловая скорость ротора, прн кото-ров амплитуда ЭДС враще-Hfi фазы равна

Цлщ ШД с раэъополириой коммутацией равна мошио-сти, потребляемой от сети в статике. Ге. мощности КЗ

ЭДС вращения фазы ррв элтрической угловой ско-

рости. чн&гё&яЬ ptfBOV

Устаиовивдавеся режимы работы шагового привода можно прертавнть в виде двух соетявлЯ1бщих дввженн: ейигрояного вращения с установившейся скоростью Ь = const И колебаний Лш относительно установившейся ckqpqpth, Прв малых колебаниях скорости ш может быть использоввн метод наложения и каждая составляющая рассматривается от-дфльво. Определение характеристик ШД прв допущеяпн постоянства скорости справедливо здшь дли областей средних и высоких ча-еют где колебания скорости малы и требуют учета только первых гармоник фазных на-пряюиий, т. е. ничем ие отличаются от ана-лорицх реКимсж работы обычного снн-хровяого двигателя (см. § 3.1.7). Для нссле-доваяий характеристик ШД и установившихся режимах прн указанных выше допущениях прнгодньвое метбдУ, разработаицё применительно к снихрояным даигателям.

Практнчесваге Я1чювя анализ уста-яовившихся режимов работы шагового привода при прииахмх допущениях ие имеет, поскольку aa.Tfiysatm учет свойств блока управления, без которого характеристики ШД. полудмыг pafWTHUM яутем, резко отличаются от реальных. Дай инженерных

ра(четов установившихся режямвЬ работы ШД использукпся эксаериментальяо полученные предельные нагрузочнклё xapaicrepH-стики УИн = ф (/). представляющие сотой зависимость предельного вюмеНта, развиваемого двигателем (при управлении от <Mipe-деленного блока) в рабочий диапазоне чаят.

Переходные процессу Ш1ГовЬм поводе. Различают два вида л1бходных. iipe-цессов в шаговом приводе: при скачхообрз-иом измеиенин частоты управляющих импульсов; при программиррваннрм ишёвё-ини частоты управления.

Первый способ уйфдвлеяия не накладывает никаких отравйчепвй яа aairaH изменения чгк:тоты уйравляюшкх импульсов и щя-меняется при работе шагового ЬрйВода в ластя частот пркёмйстЪстя /пп, под понимают максимально до11}нмый частот, не прийодяця квыпaдеifIню Щ сийхроййзма, второй способ, xapasfip: иаменвКнём частоты управовн по Ие иу закону, скорость изменения частей котором обеспечивает сЬакеиие BQCTH ШД и ис1ючает iioTcp инф

Прн первом способе управляй определяютсй тастотяые и скбростяые два-

Т щ,6 л. а, а а ?.в. ртиосат { яыв мкницы

Назваяне

Обоэнечевве

Способ вычвслевня, фориуле

Пояснения и прмч -ччн

BpjftfiiepH; BpeifB Вюреэмериея ча-

шаразмервое на-

npjiJkeBHe ялв функция воздействия

зреэигернвв ИЛИ элек Ьяческя коврдвяж? -

Вараанерная пв-стоавиая времена

Веэразмериое внут-

№яоап аьиая

Отноеятельиея ме-М уга1}вая

Йа МОП

i, - (f.) Т.

-Tr .rf-trf/f6=?? -

<)/ б ~ < - в)

Рб tl.

Л*н.-и/Л*б Мт.-М,/Л*б; В I <(в

вм/б.-

Всегда I *. и,\ < l

Всегда I i. 1 < I

В преобразоранных vpan-нениях пав < тр-), epj. -териэует пОстоЯКИце iniWMt- В (или их компрнеяты (. моток аре9бпвзо8 ттзгс 1!)Л и выряжен через первой а-чеЛьвые фй1иые gajvTHh-носта >

Одяовремеино параметр Н можно пкмв -как отво-свтедьную ЭДС зращенвя

Всегда М < 1

паэс (от щуйя ДО некоторого предельного знач№и ), в которых ЩД мржет выполнять все цли некоторое юман; пу к, осташвку. реверс, ;Кзмекеннв скорости (частоты). Занв-симастигра1}1<)ных частот внезапного пуска (или* рркшисюти) fnp, и реверса fp, от обобиКых параметров я, Т А4, определяют предельные динамические характеристик! в1ШВояа (ем. ряс. 3.47). Завиеимосга /вр*. /р. (п. Тф. Л1в,) от обобщенных .Rjif !P<№. Э))Д9ни № ек лят1че<}й1 ив в 1 !1рад4Х, Лприврдятоя ддя мялектяо поставляемых щпмшрв в обл частот < ?пр и / < р... рторых црнвод без ШШ С даполн?ет указаям*

команды.

Нахождение шмных зависимостей F(n, Г £ ,)требует численного Hwferpn-роиаиия полных Уфвиенвй даижения и выполняется на АЕМ (лбо экспериментально).

Изменение 3стдты управлений ШД по программе Mo%ef пронавоться либо плавно, либоскачками. Кк правило; используются линейный н эксцненкцальный законы изменения чаеоти управления, обеспечивающие близкие к оптимальным по быстро-дейсгтю выходные яропоесы.

Оптимальный вывод иа режим для каж-J№FQ.ee4 7W пвдаА}1§тров Г., Я M , g частоты установившегося режима / яре Я Ше Р.ср%> fSitf9pM(jTejibHyro задачу, iRlie jp§fl.MffiR.6jiiTb получено на *

Расчет KiftitreimiTiiK на Mf/LQfoOm-Н0СТ1Й0 модели ШД ямя тея с о(яшнм()гть ыоштродщтя псшояичвмвов. фумспин sin (* - vi. Нввболм р бпростр ве еяы№ ме- одем формяровйявя фуякщш n<e-v) 1вля <ip iCT uM i)fe ее в .виде

sta(e-Y) =sta в cos у-cose sin у.

Функция В0 зст я cos V к sin V являются CTyncHiaTbaffl, а число ступеней равно числу тактов коммутации п. Формир9ва)1ае функций cost и Шутя модели осуществляется ввещцим блоком упрцвлеиия ЩЦ, щл вцходе Кото)!ога:1кдарчеад pwie, переклю а1рцше в

-фний, пддаваемы)! на АВМ.

Фун1а№& sin fl и tos ff получают в результате решения на модели вспомогательной системы уравцеччй:

(sin fe,) = б сое -S йп Й/,; (cos fe,) == -т в sin , - в cos

где е - ошибка, шгорую следует снизить да дая. вч пг-- црррзврдрая угла е.

Схема модели для формирования фувкций cos в и аЗйб приведена аа рнс 8.4S,ч . Схема ррб, а.49 фор>1<ируетфу Ш1 tfsi4 в, Scps в, sin и sps i, 1Ш(>рые 1 полр>л01<ея прн щееирршш ур9рк 1Вй 4виж$кки ЩД,