в пределе, когда t- О, спектр импульса становится равномерным, а g((o) 1. Отсюда следует, в частности, известное положение, что для бесконечно короткого импульса в виде 6-функции (дельта-функции) &( )=!

Иногда важно знать, как распределяется энергия в спектре. Для этого пользуются интегральной кривой распределения [Л. 1], представляющей отнощение энергии колебаний, заключенной в интервале частот О-/, к полной энергии импульса:

Y(/)=

2\s(f)df

J а2 (t) dt

(to) da

(11-7)

a (t) dt

с помощью функции y(/) определяется активная щирина Д/и.а спектра, т. е. область частот, в которой заключена подавляющая часть энергии спектра и которая включает составляющие, решающим образом влияющие на форму импульса. Обычно активная щирина спектра определяется как область частот О - Л/и.а, причем

[Y(/)]f=f ., = 0,95.

Для определения активной ширины спектра импульсов =Д/и.а любой гладкой формы (без наложенных высокочастотных составляющих) служит универсальный график на рис. 11-8. Здесь Afn.a равна полосе частот, в пределах которой сосредоточено 95% энергии спектра.

Приближенно для импульсов любой формы можно считать, что величина Д/и.а связана с длительностью импульса соотношением

где /Сс0 = 1,4-:-2,5, причем чем меньше отношение /ф.а/и, тем больше коэффициент Ксп из указанного диапазона (см. также § 2-2).

В теоретических исследованиях часто для простоты полагают приближенно/Ссп=1.

Спектр периодической последовательности радиоимпульсов легко определить по спектру огибающей (видеоимпульса). Для наиболее часто встречающегося в практике случая, когда длительность импульса много больше периода несущей частоты (/и>1 н), т. е. при условии, что в импульсе содержится большое количество периодов несущей частоты, амплитудный

спектр радиоимпульса состоит из несущей /н, по обе стороны которой симметрично располагаются гармоники, повторяющие спектр огибающего видеоимпульса. Спектральная функция радиоимпульса Sp((o) имеет ординаты, в 2 раза меньшие ординат спектральной функции s((o) видеоимпульса (рис. 11-9). Подобным же образом строится фазовый спектр радиоимпульса.

tu ° и tu tu

Рис. 11-9. Спектр последовательности радиоимпульсов Sp(/) длительности с частотой повторения Ff, прн условии, что Tjj< Т-

Согласно изложенному связь между комплексными спектральными функциями радио- и видеоимпульсов при tl/f выразится так:

р(м) = -8(м- н)е*( - и), (11-8) где

сй = 2я/ .

Спектры некоторых видеоимпульсов

Импульсы прямоугольной формы. Спектральная функция и относительная спектральная функция

S (to) = г/и -~- =

nftn Otn

-Untn

I sin tn I nftn

sin-

sin-

(11-9)

обращаются в нуль на частотах f=llta, 2 и, 3/<и ... (рис. 11-10, а). Величина каждого последующего максимума меньше предыдущего; .они относятся как 1 : 0,21 : 0,13...

Так как 957о энергии импульса заключено в полосе д/и.а=2 и, то для прохождения видеоимпульса длительностью без существенных искажений линейная система должна иметь полосу пропускания В

>Afn.a=2 .

Фазовый спектр последовательности прямоугольных импульсов (рис. 11-10,6)

представляет собой ступенчатую кривую с изменением фазы на угол п в точках /= =k/tB,k = l,2...

Если начало координат совместить не с серединой, а с началом импульса, то фазовый спектр будет иметь форму пилообразной кривой с тангенсом угла наклона каждого зубца я/и и периодом (рис. 11-10,6).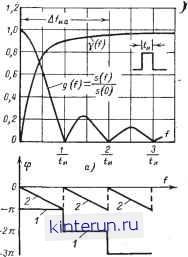

Рис. 11-10. Спеетр видеоимпульсов прямоугольной формы.

а - относительная спектральная функция и интегральная кривая распределения энергии Т для определения ширины энергетического спектра; б - фа- зовый спектр для случая, когда начало координат t-=0 совмещено со срединой импульса (/) и началом импульса (2).

Импульсы треугольной формы. Спектральная функция (рис. 11-11) и относительная спектральная функция имеют вид;

s (w) = --- 4

- cos

/, и

1 - COS

Энергетическая полоса 0.5

(11-10)

А/и.а = - = Ги

9 где ?и.а - активная длительность

импульса.

Импульсы колокольной формы. Импульс описывается выражением

-2,77 -

a(t) = Ae-*=Ae

причем параметр Р, характеризующий ширину кривой a(t), связан с активной длительностью импульса равенством

1,67

Спектральная функция (рис. 11-12)

/я -

S((0) =

4Р

= l,374,S-3.55( t.fY .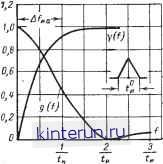

Рис. 11-11. Относительная спектральная функция g(f) и интегральная кривая распределения энергии V треугольного импульса.

Так как s (0)

g((0) = e =е-3-65( W)= . (1М1>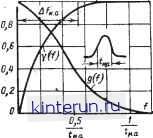

Рнс. 11-12. Относительная спектральная функция sif) и интегральная кривая распределения энергии 1 (f) колокольного импульса.

Активная ширина спектра А/и.а=0,52/Л,. Фазовая характеристика совпадает с-осью частот, т. е. ф((о)=0.

11-3. ПРОХОЖДЕНИЕ ИМПУЛЬСОВ ЧЕРЕЗ ЛИНЕЙНЫЕ ЦЕПИ

Основные методы анализа переходных процессов

В импульсной технике широкое применение находят в основном три метода: спектральный, операционный и суперпозиционный.

Спектральный метод основан на суммировании результатов прохождения каждой гармонической составляющей спектра вход-чюго сигнала через линейную цепь.

Если спектральная функция входного

импульса a(t) равна s((o), а комплексный коэффициент передачи (или частотная пере-

.даточиая функция) цепи равен K(j(i>) = =/С((о)е , то выходной сигнал 6(() выражается формулой (см. § 5-2)

b(t)--

2я .

s(£o)A(/£o) e *dco =

5(£0) К((>>) е * +* ( >+ dw.(11-12)

Отсюда следует, что модуль спектральной функции меняется в К(а>) раз [он становится равным /C((o)S(£o)], а фаза сдвигается на угол ф((о) и становится равной ф((о)-Ь

В том случае когда входной сигнал периодический, выходной сигнал представляется в виде бесконечного тригонометрического ряда

= S -Kimekt , (11-13)

который получается из ряда (11-2) путем умножения комплексной амплитуды каждой тармоники спектра на коэффициент передачи (/ )/ш=£з цепи, соответствующий дан-

ной гармонике.

Для некоторых типов входных сигналов :ряд (11-13) может быть конечным.

Рядом (11-13) пользуются обычно для -теоретических исследований, приближенного (качественного) анализа, а также в тех сравнительно редких случаях-, когда вычисление интеграла (11-12) или ряда (11-13) яе представляет больших трудностей, и для точного количественного анализа.

Операционный (или операторный) метод основан на использовании преобразования Лапласа для функции a{t) (см. § 5-2)

А(р)=\ a{t)e-P*dt, (11-14) О

тде p=a+i - некоторое комплексное чис-.ло, называемое параметром преобразования. Функция А(р) существует для импульсов

любой используемой на практике формы, причем интегрирование производится на участке <и, поскольку вне его с(()=0.

По известному преобразованию А(р) можно найти исходную функцию по формуле обратного преобразования Лапласа

а()=-

,-1-/0,

A{p)eUp,

(11-15)

в котором интегрирование производится вдоль прямой о, параллельной мнимой оси, проходящей правее всех полюсов функции А(р).

Для многих видов функций имеются заранее вычисленные таблицы прямого и обратного преобразований Лапласа (см. § 1-10, 5-2).

Практически при использовании этого метода для анализа действия импульса на электрическую цепь каждый из элементов цепи заменяется * операторным сопротивлением: конденсатор 1/Ср, индуктивность Lp, резистор R. Затем записываются законы Кирхгофа для цепи, причем входное напряжение или ток заменяется операторным выражением, найденным по формуле (11-14) или по таблицам. Решая полученное алгебраическое уравнение, находят операторное выражение для искомой величины В(р), а затем, пользуясь формулой обратного преобразования или таблицами, определяют саму величину b{t).

При использовании описанного метода электрическую цепь характеризуют передаточной функцией W(p), равной отношению преобразования Лапласа выходной величины к входной.. Обычно W(p) является отношением двух полиномов

W(p) =

N(p)

(11-16)

причем степень полинома числителя ие пое-восходит степени полинома знаменателя. Если на вход цепи действует сигнал a(t), то преобразование Лапласа выходного сигнала равно:

B(p)==A(p)W(p). (11-17)

Выходной сигнал находится как обратное преобразование от В(р), т.е.

e-f-jm

b(i) = -~ f B{p)ePUp=

c-fm

= f (P) W{p)ePdp, (ll-17a)

C-jm

где интегрирование производится по прямой, параллельной мнимой оси, располо-

* Для простоты эти правила приводятся для нулевых начальных условий. Соответствующие правила для ненулевых начальных условий приведены в [Лг 1].